
Zie ook Help voor meer informatie. We zien wel...:-)


Minder contexten in de rekentoets, meer opgaven die zonder rekenmachine gemaakt moeten worden, meer herkansingen en minder zware weging bij het eindexamen. (...) Over het nut van een afzonderlijke rekentoets zijn de meningen verdeeld.Dat wisten we eigenlijk al toch? Je kunt natuurlijk niet alle mallotige maatregelen terugdraaien? Of toch wel? Zullen we ons verstand 's gaan gebruiken? 't Is maar een idee.

Het heeft wel even geduurd voordat ik door had wat hier nu precies mis ging:-)
Een onderzoeker vermoedt dat de kans om met een dobbelsteen een ‘zes’ te gooien niet 1/6 is maar kleiner. Hij vermoedt dat dit komt doordat er bij de ‘zes’ de meeste kuiltjes zitten en deze kant van de dobbelsteen een beetje ‘lichter’ is dan de andere kanten van de dobbelsteen.Daar klopt iets niet. Dat was tot nu toe kennelijk niemand opgevallen. Tot vandaag dan... Via de e-mail:
Is het niet zo, dat als de dobbelsteen aan de kant van de 'zes' (als die al lichter zou zijn!) juist vaker boven zou komen te liggen? Dus die kans zou juist groter moeten zijn dan een zesde...Lijkt me ook ja:-)
met vr.groeten k
Hij vermoedt dat dit komt doordat er bij de ‘zes’ de meeste verf zit en deze kant van de dobbelsteen een beetje ‘zwaarder’ is dan de andere kanten van de dobbelsteen.Dat is ook onzin, maar vooruit, je bent onderzoeker of niet...:-)
 |
klas 2 |  |
|
 |
klas 2 |  |
|

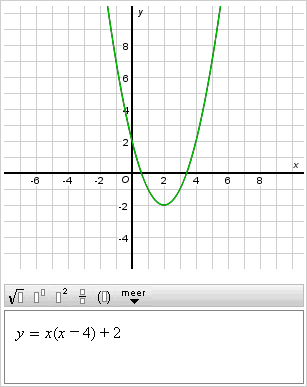
Als je nu denkt: 'de grafiek van y=√x' is gespiegeld in de y-as en '3' naar links verschoven ga je te kort door de bocht.

Op deze pagina kan je een overzicht vinden met een samenvatting van de transformaties.
Wat blijkt? De grafiek van y=√-x wordt juist naar rechts verschoven. Nou ja...:-)
Hoe zit dat?
...
Dat was dan toch wel weer een mooi moment...
C. zei nog 'volgens mij klopt het niet hoor', maar de juffrouw achter de kassa wist het zeker: 'nee hoor, het klopt'. Nou dan niet... hebben wij gratis bier vandaag:Graag of niet, denk ik dan maar. Iedereen heeft recht op z'n eigen blinde vlek.

Lekker is dat...:-)
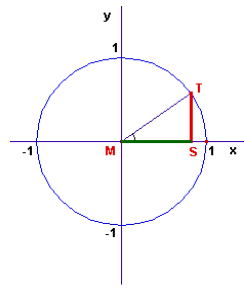 In de vijfde klas moesten we hoofdstuk 8 goniometrie nog afmaken. Leerlingen vinden dit een moeilijk hoofdstuk. Dat klopt. Ik denk het moeilijkste hoofdstuk van klas 4 en 5, inderdaad. De vraag is: waarom is dat?
In de vijfde klas moesten we hoofdstuk 8 goniometrie nog afmaken. Leerlingen vinden dit een moeilijk hoofdstuk. Dat klopt. Ik denk het moeilijkste hoofdstuk van klas 4 en 5, inderdaad. De vraag is: waarom is dat?
De eenheidscirkel en radialen zijn echt een nieuwe manier om naar goniometrische verhoudingen te kijken. Hoeken zijn niet meer een maat voor de grootte van een hoek maar 't is eigenlijk een variabele. De sinus, cosinus en tangens zijn eigenlijk functies. Periodieke functies zelfs. Dat is alles bij elkaar al lastig...
In paragraaf 3 komen transformaties en sinusoiden aan bod. Die transformaties hebben we gehad, maar die waren de eerste keer ook al lastig en 't is maar de vraag of iedereen dat nu helemaal begrepen had. Maar die 'voorkennis' heb je bij transformaties en sinusoiden wel hard nodig. Dus als je die voorkennis niet helemaal goed verwerkt hebt wordt het lastig...
Eén van de thema's bij wiskunde B is het oplossen van vergelijkingen. In vrijwel elk hoofdstuk kom je dat tegen. Lineaire, kwadratische, wortels, exponententiele, logaritmische, ... en dan in hoofdstuk 8. De goniometrische vergelijkingen. Die zijn verreweg het lastigst. Vooral omdat je allerlei kunststukjes moet uithalen omdat je steeds te maken hebt met oneindig veel oplossingen. Meestal heb je twee fundamenteel verschillende oplossingen die van zichzelf ook uit oneindige veel oplossingen bestaan. Het rekenen en opschrijven behoeft extra aandacht.
In de laatste paragraaf gaat het om de afgeleide van goniometrische functies. Dus daar kom je dan weer de productregel en de kettingregel tegen. Dat was de eerste keer ook al lastig maar is als voorkennis voor deze paragraaf een 'abolute must'.
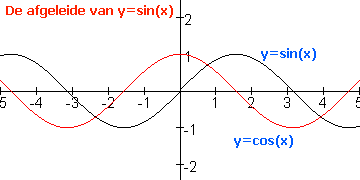
Ik denk dat als je hoofdstuk 1 tot met 7 helemaal begrepen had en de stof volledig zou hebben verwerkt dat je met hoofdstuk 8 veel minder moeite zou hebben. Je begrijpt al dat dit in de praktijk niet zo zal zijn. Anders had iedereen alleen maar tienen gehaald.:-)
Maar... je kunt er wel iets van leren. Voordat je nu 'stuk bijt' op hoofdstuk 8 ga eerst hoofstuk 5 t/m 7 herhalen! Zorg dat je weet hoe het zit met de transformaties, de vergelijkingen en de afgeleide.

Voor ieder wat wils. Er zijn (nog steeds) verschillende gebruikers en die moet je 't natuurlijk altijd zo gemakkelijk mogelijk maken. Met je smartphone wordt je meteen doorgestuurd naar de 'mobiele versie', dus dat is dan ook nog handig. De website staat weer open. Waarschijnlijk zal ik het toch weer moeten gaan gebruiken. Hoeveel websites heb je nodig?:-)

't Is een hele verzameling, inmiddels. Op die manier houd ik nog een zicht op alles wat ik zo gebruik. Ik geef toe, veel plannen, veel oude dingen, maar uiteindelijk erg handig voor mezelf. En daar gaat het om...:-)
"WisFaq is vooral bedoeld voor leerlingen uit het voortgezet onderwijs in Nederland en België. Anderen mogen wel vragen stellen, maar deze vragen worden soms wel maar soms ook niet beantwoord."Maar er zijn grenzen. Soms krijg ik wel 's het idee dat er mensen zijn die een leuke discussie willen beginnen, bijvoorbeeld over vakdidactiek. Ik moet me dan altijd inhouden.
De verleiding om leerlingen 'handige truukjes' te leren is groot, maar dat gaat op termijn eerder tegen ze werken dan in hun voordeel. Op de korte termijn geeft dan misschien betere resultaten maar 't is bouwen op drijfzand en vragen om moeilijkheden.
Een voorbeeld van zo'n 'truuk' is bijvoorbeeld 'het omrekenen van meters per seconde naar kilometer per uur'. Je kunt leerlingen er op wijzen dat als je de snelheid in meter per seconde vermenigvuldigt met 3,6 dat je dan de snelheid in kilometer per uur krijgt. Op de korte termijn werkt dat prima, maar, je snapt wel, na een maand of wat is de truuk vergeten. Was het nu vermenigvuldigen of delen? Was het nu 3,2 of zoiets? Dat is niet handig. Dan maar liever op deze manier. Eigenlijk heb je daarna geen truuk meer nodig.
Zo vind ik bij het oplossen van vergelijkingen de methode 'overbrengen en dan verandert het teken' wel een heel mooi voorbeeld van een verkeerde truuk. Een vergelijking bestaat uit een linker- en een rechterlid met een =-teken ertussen. Dat betekent dat links en rechts hetzelfde 'getal' staat. Als je nu maar links en rechts dezelfde bewerking(en) er op uitvoert kan het bijna niet fout gaan. De vraag is dan niet 'mag dit?' maar 'klopt dit?'.
Maar sommige mensen willen gewoon graag 'dingen' van rechts naar links overbrengen en wel zo dat het teken verandert. Maar wat is dat voor iets?:-) Dat zal op de korte termijn misschien wel werken, maar 't is echt flauwekul. Wie verzint er zoiets?
Als je nu leerlingen (bij-)les geeft probeer dan een beetje verder te kijken dan de korte termijn. Die leerling wil graag een snelle en vooral makkelijke oplossing, maar een goede leraar kijkt verder dan de korte termijn. Betere resultaten wil dus niet per sé zeggen de cijfers op de eerstvolgende toets, maar zou wel 's het succes in een later stadium kunnen zijn.
Dat je dat maar weet...:-)
Opgave 1.
Los op:
a. x²-5x-24=0
b. a²+8a-48=0
c. 6x-16x²=0
Opgave 2.
Los op:
a. (x-4)(x-6)=48
b. (x-2)(x+9)=12
c. (x-5)(2x+3)=0
Bij opgave 1. weet je dat c. problemen gaat geven. O ja, je moet iets met 'x' buiten haakjes halen. Dat is al even een stap. Daarna zijn er nog een paar problemen:
6x-16x²=0
2x(3-8x)=0
2x=0 of 3-8x=0
Zowel '2x=0' als '3-8x=0' is een probleem. Een aantal leerlingen weet niet hoe 't verder moet. Dat is bijzonder want dit zijn 'gewoon' twee lineaire vergelijkingen. Zie hoofdstuk 2 en klas 1.:-)
Kennelijk is er het ontwikkelen van het idee over 'doe links en rechts hezelfde' niet veel terecht gekomen. Op die manier wordt er niet veel opgebouwd aan de begripsvorming en blijven de vaardigheden voor het oplossen van vergelijkingen achter.
Bij Opgave 2. ligt bij c. het voor de hand dat leerlingen gaan proberen de haakjes weg te werken en dan proberen te ontbinden in factoren. Dat is nu jammer, want dat stond er al. Ook in dat geval moet ik vaststellen dat het idee van 'ontbinden in factoren' en 'iets keer iets is nul' ook al niet veel terecht gekomen is.
Ik kan niet anders concluderen dat leerlingen vooral 'truukjes' leren. Er is weinig samenhang. Dat is geen wiskunde. Dat moet anders. Anders komen we nooit ergens. Je kunt het de leerlingen niet echt kwalijk nemen, denk ik. Kennelijk slaagt het boek (en de docent) er (nog) niet in om nu precies duidelijk te krijgen hoe het nu allemaal precies in elkaar steekt.
Wiskunde leer je door te doen, inderdaad. Dus het boek/docent moet eerder beginnen met gemengde opgaven en meer focussen op 'begrijpen wat je aan het doen bent'. Dat betekent meer tijd inruimen voor de verwerking. Het liefst voor de proef en niet er na...:-)
De vraag is dan even hoe dat dan moet?

Je moet daarbij alle kennis over getallen en rekenvaardigheden uit de kast halen en als je maar steeds 'logisch' blijft dan krijg je dat (soms) nog voor elkaar ook. Tada! Weer een vergelijking opgelost.
Maar ja, getallen zijn mijn vrienden, dus ik vind dat leuk:-)
Zie ook Math doesn't suck you do of leesmapartikel voor een meer 'no-nonsens-benadering'...:-)
Foto's staan in de werkruimte op wiskundeleraar.nl. Een aantal staan ook op de projectpagina/weblog.
Naast het normale programma waarin de leerlingen kennis en vaardigheden opdoen is het niet zo'n gek idee om ook andersoortige opdrachten aan te bieden. Het doel van wiskundeonderwijs is niet het halen van proeven en examens. Uiteraard is een diploma wel een bewijs dat er sprake is geweest van het volgen van onderwijs maar de doelen gaan hopelijk wel iets verder.
In het kader van het ervaren van de nut en noodzaak van de wiskunde kan je opdrachten aanbieden die proberen de kennis van de wiskunde te verbreden of te verdiepen. Hieronder kan je daar een aantal voorbeelden van vinden:
 De som en het product van twee getallen
De som en het product van twee getallen Ik stel me zo voor dat bij de evaluatie van de opdrachten verschillende werkvormen kunnen worden ingezet. Je kunt het naar behoren uitvoeren van de opdrachten waarderen met tijd waarbij leerlingen een bepaalde tijd moeten besteden aan extra opdrachten of gewoon cijfers geven die meetellen. Montessorigewijs kan je bij deze opdrachten de nodige keuzevrijheid geven.

 In de tweede klas gaan de MAVO-leerlingen in plaats van de proef van hoofdstuk 5 maar 's een keer iets anders doen. Laat ze maar 's nabouwen met drie of twee aanzichten in DWO. 't Is dan wel handig als ze in wiskundeleraar.nl een werkruimte kunnen vinden met de nodige informatie. Daar kunnen ze ook aangeven als ze de opdracht gedaan hebben. Ik kan dan gaan kijken of het gelukt is en de opdracht afvinken en eventueel van feedback voorzien.
In de tweede klas gaan de MAVO-leerlingen in plaats van de proef van hoofdstuk 5 maar 's een keer iets anders doen. Laat ze maar 's nabouwen met drie of twee aanzichten in DWO. 't Is dan wel handig als ze in wiskundeleraar.nl een werkruimte kunnen vinden met de nodige informatie. Daar kunnen ze ook aangeven als ze de opdracht gedaan hebben. Ik kan dan gaan kijken of het gelukt is en de opdracht afvinken en eventueel van feedback voorzien. In de derde klas kan je leerlingen tegen komen die er niets van bakken. Ze willen misschien wel, maar 't lukt niet, dus doen ze maar niks, want dat heeft toch geen zin. Dat kan je natuurlijk niet goed vinden. Ik ben gestart met een soort bezemklas. 't Idee is om te om hoofdstuk 5 (HAVO) en hoofdstuk 4 (VWO) nu 's een keer wel goed te doen. 't Zijn typische wiskunde A hoofdstukken dus als ze nog iets willen dan zullen ze in de meeste gevallen in ieder geval wiskunde A gaan doen. Als dat hoofdstuk lukt dan is dat alvast weer een positieve ervaring, maar dan kunnen ze voor de hoofdstukken die ze erbij hebben laten zitten andere activiteiten doen. Dat moeten dan 'handige manieren' zijn om voldoende kennis op te doen die ze in de 4e klas nodig hebben.
In de derde klas kan je leerlingen tegen komen die er niets van bakken. Ze willen misschien wel, maar 't lukt niet, dus doen ze maar niks, want dat heeft toch geen zin. Dat kan je natuurlijk niet goed vinden. Ik ben gestart met een soort bezemklas. 't Idee is om te om hoofdstuk 5 (HAVO) en hoofdstuk 4 (VWO) nu 's een keer wel goed te doen. 't Zijn typische wiskunde A hoofdstukken dus als ze nog iets willen dan zullen ze in de meeste gevallen in ieder geval wiskunde A gaan doen. Als dat hoofdstuk lukt dan is dat alvast weer een positieve ervaring, maar dan kunnen ze voor de hoofdstukken die ze erbij hebben laten zitten andere activiteiten doen. Dat moeten dan 'handige manieren' zijn om voldoende kennis op te doen die ze in de 4e klas nodig hebben.  In de tweede klas ga ik ook zo iets doen. Ik ga proberen om met name DWO in te zetten om leerlingen weer een beetje op 't spoor te krijgen. Algebraische vaardigeheden, grafieken tekenen, formules...
In de tweede klas ga ik ook zo iets doen. Ik ga proberen om met name DWO in te zetten om leerlingen weer een beetje op 't spoor te krijgen. Algebraische vaardigeheden, grafieken tekenen, formules... Ik ga proberen om wiskundeleraar.nl wat meer in te zetten voor mijn eigen onderwijs. Er zijn werkruimten voor 2a/2b, 3E en HAVO 4. In een werkruimte kunnen leerlingen dan alle informatie vinden: samenvattingen, proeven en uitwerkingen, extra lesmateriaal, uitleg, opdrachten, presentaties, forum, …
Ik ga proberen om wiskundeleraar.nl wat meer in te zetten voor mijn eigen onderwijs. Er zijn werkruimten voor 2a/2b, 3E en HAVO 4. In een werkruimte kunnen leerlingen dan alle informatie vinden: samenvattingen, proeven en uitwerkingen, extra lesmateriaal, uitleg, opdrachten, presentaties, forum, …