De gegevens van zondag 29 december 2013:
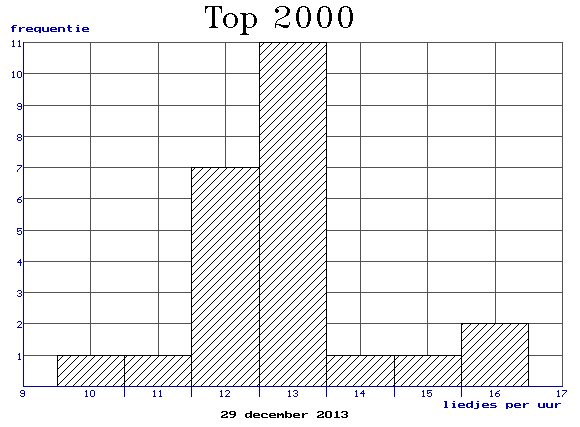
Als het goed is dan is het gemiddelde ongeveer gelijk aan 12,8 liedjes per uur.


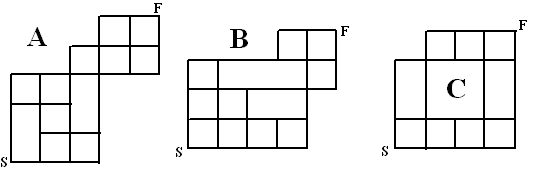
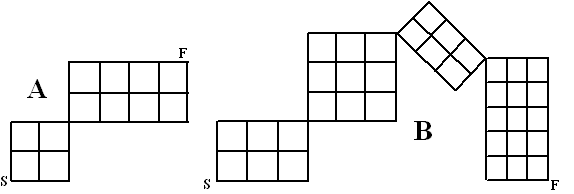
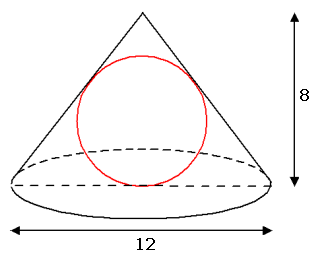
Een bak in de vorm van een balk met lengte 10 m, breedte 10 m en
hoogte van 1 m moet bollen bevatten met een diameter van 1 m.
|
 |


 Voor opgave 4 van de proef van hoofdstuk 2 kun je 6 punten halen.
Gemiddeld scoren de leerlingen 1 punt. Eén leerling scoort 6 punten, één
leerling scoort 3 punten, 5 leerlingen 2 punten en één leerling 1 punt. De rest
heeft geen punten.
Voor opgave 4 van de proef van hoofdstuk 2 kun je 6 punten halen.
Gemiddeld scoren de leerlingen 1 punt. Eén leerling scoort 6 punten, één
leerling scoort 3 punten, 5 leerlingen 2 punten en één leerling 1 punt. De rest
heeft geen punten.


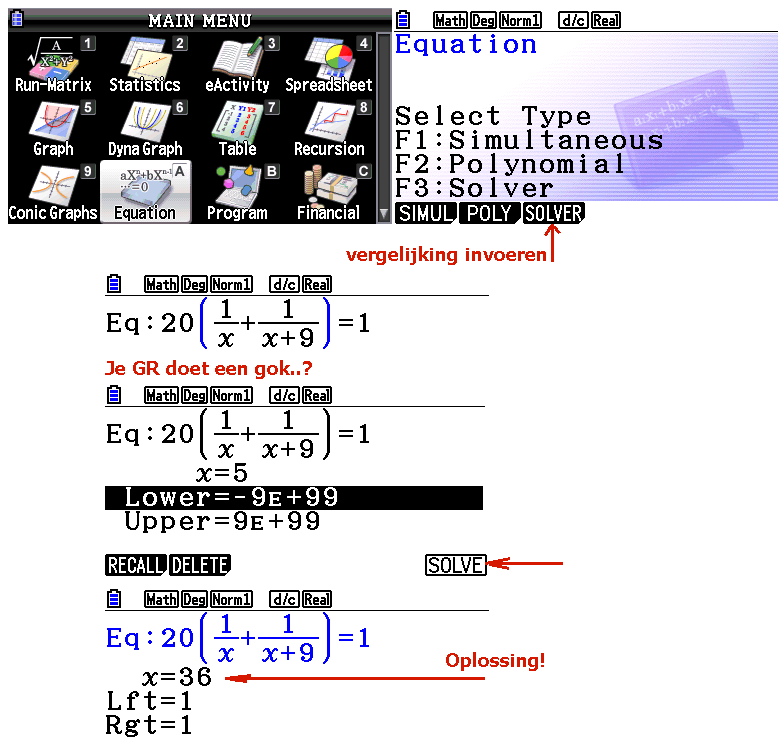

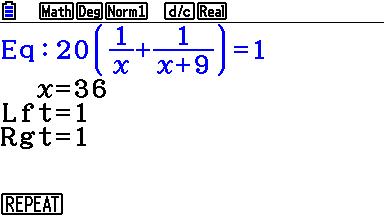



Als je twee breuken wilt optellen dan maak je de breuken gelijknamig en dan kan je ze 'onder één noemer zetten' en optellen.
\(
\Large\frac{2}{3} + \frac{2}{7} = \frac{{14}}{{21}} + \frac{6}{{21}} = \frac{{20}}{{21}}
\)
Daar zou je best een rekenregel voor kunnen verzinnen. Je kunt tellers en noemers kruislings vermenigvuldigen, die optellen en delen door het product van de noemers:
\(
\Large\frac{2}{3} + \frac{2}{7} = \frac{{2 \cdot 7 + 2 \cdot 3}}{{3 \cdot 7}} = \frac{{14 + 6}}{{21}} = \frac{{20}}{{21}}
\)
Zo'n rekenregel voor het optellen van breuken kan handig zijn, bijvoorbeeld bij het onder één noemer zetten van gebroken termen met variabelen:
\(
\eqalign{
& \frac{x}
{{x - 1}} + \frac{{x^2 }}
{{x + 3}} = \cr
& \frac{{x(x + 3) + x^2 (x - 1)}}
{{(x - 1)(x + 3)}} = \cr
& \frac{{x^2 + 3x + x^3 - x^2 }}
{{(x - 1)(x + 3)}} = \cr
& \frac{{x^3 + 3x}}
{{(x - 1)(x + 3)}} \cr}
\)
Bij zo'n rekenregel hoef je dan verder niet na te denken. Het antwoord rolt er, als het ware, bijna vanzelf uit.
Toch kom je die rekenregel zelden tegen. Er is, denk ik , een goede reden om dat ook niet te willen. Het is veel handiger om gelijknamig te maken. Dat werkt bij formules hetzelfde als bij getallen, dus waarom zou je een rekenregel moeten leren als je die helemaal niet nodig hebt?
Rekenregels, stappenplannen en ezelsbruggetjes hebben de neiging te worden vergeten, verhaspeld of op het verkeerde moment van stal gehaald. Dat is ook iets wat je niet moet willen. Jammer is het wel. Ik vond het bij de gebroken termen wel handig ergens.:-)
Bij HAVO wiskunde B gebruiken we hier en daar ook een soort van rekenregels. Die regels kan je dan uit je hoofd leren en op het goede moment inzetten:
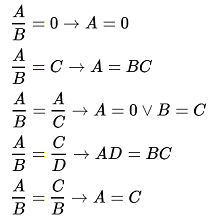
Maar zijn die nu eigenlijk noodzakelijk? Zou je niet gewoon moeten weten hoe dat werkt en zelf bedenken hoe 't zit bij die gebroken vergelijkingen? Zou dat niet veel beter zijn?
Als je eenmaal dingen begrijpt hoef je nooit bang te zijn dat je iets kwijt raakt. Het zit gewoon tussen je oren...:-)
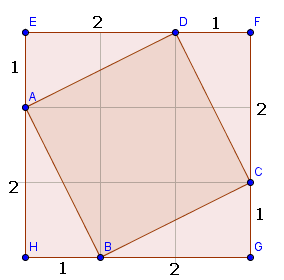
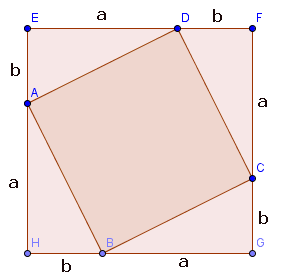








 1. Probleemaanpak
1. Probleemaanpakfunction ggd(a,b)
a = abs(a)
b = abs(b)
if a = 0 then
ggd = b
else
if b = 0 then
ggd = a
else
if a > b then
ggd = ggd(b, a mod b)
else
ggd = ggd(a, b mod a)
end if
end if
end if
end function
function kgv(a,b)
kgv=a*b/ggd(a,b)
end function