woensdag 30 januari 2013
zaterdag 26 januari 2013
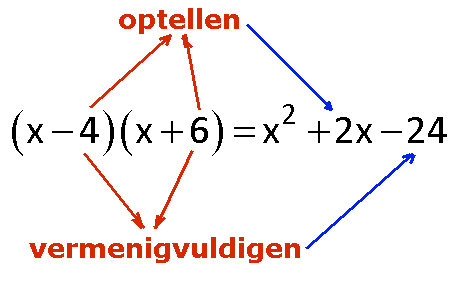
Wat hoort bij wat?

Zie ook:
Vraag van de avond:
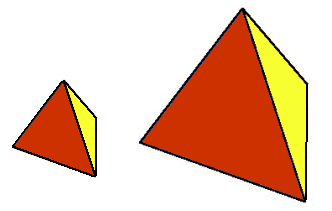
Hoeveel keer zo groot is de rechter figuur?
Tenslotte:
...en niet vergeten: aan het begin van de avond ligt al het klikmateriaal los op de tafels. Aan het eind is er geen los stukje te bekennen. Als dat geen voorbeeld is van afnemende entropie dan weet ik het ook niet...:-)
Voor de rest? Gewoon erg leuk. Leerlingen komen niet naar het HML omdat we een normale school zijn, denk ik...:-)
zaterdag 19 januari 2013
Wiskunde en konijnen
 Leerlingen in 5 havo wiskunde B die hun PO (nog) niet hebben gedaan kunnen de cursus 'wiskunde en konijnen' doen. In deze 'minicursus' maak je kennis met formules, variabelen, grafieken, de rij
van Fibonacci, getallenstelsels en groeimodellen.
Leerlingen in 5 havo wiskunde B die hun PO (nog) niet hebben gedaan kunnen de cursus 'wiskunde en konijnen' doen. In deze 'minicursus' maak je kennis met formules, variabelen, grafieken, de rij
van Fibonacci, getallenstelsels en groeimodellen. Aanwijzingen volgen nog via de verzendlijst in de werkruimte. Op deze beschrijving in WisKast vind je meer informatie. Op dit weblog zal ik af en toe 's schrijven hoe dat gaat, wat de ervaringen zijn en hoe 't afgelopen is. Misschien ga ik er zelfs wel over publiceren in één van de vakbladen.
Vooruit maar! Als je niet verdwaalt dan vind je nooit een nieuwe route...
Schapen
Ik heb een keer uit rekenbeter.nl dit sommetje opgeduikeld:
Zie ook Getallenstelsels. Slaapverwekkend...:-)
Een aardig sommetje om het werken met variabelen toe te lichten. Neem voor het aantal schapen 'n' en dan volgt de rest vrij makkelijk vanzelf.Een boer zegt tegen een schaapherder: "Waar ga jij met die 100 schapen naartoe?" De schaapherder zegt: "Het zijn er bij lange na geen 100. Dan moet er eerst net zoveel bij, dan nog half zoveel dan nog een kwart zoveel en," zegt hij tegen de boer, "dan moet je er zelf ook nog bij gaan lopen. Dan heb ik pas 100."
Zie ook Getallenstelsels. Slaapverwekkend...:-)
woensdag 16 januari 2013
donderdag 10 januari 2013
Breuken
Ik had zomaar een voorbeeld genomen. Eerst voor het optellen van breuken en daarna met dezelfde breuken vermenigvuldigen van breuken. Ik had daarvoor 2/3 en 3/4 genomen. Je moet natuurlijk ook gemengde breuken kunnen vermenigvuldigen. Daarvoor had ik, om op één lijn te blijven, 22/3 en 33/4 genomen. En wat denk je? Komt gewoon 10 uit:-)
NASCHRIFT
Meer algemeen?
Zou 33/4·44/5 ook leuk uitkomen?
Ja, er komt 18 uit.
a=2 geeft 10
a=3 geeft 18
a=4 geeft 28
a=5 geeft 40
...
Algemeen: a geeft a(a+3)
NAGEKOMEN BERICHTEN
Zie ook breuken op wiswijzer
NASCHRIFT
Meer algemeen?
Zou 33/4·44/5 ook leuk uitkomen?
Ja, er komt 18 uit.
a=2 geeft 10
a=3 geeft 18
a=4 geeft 28
a=5 geeft 40
...
Algemeen: a geeft a(a+3)
NAGEKOMEN BERICHTEN
Zie ook breuken op wiswijzer
Combinaties en permutaties
Deze oefening bestaat uit een aantal vragen over 'combinatie en
permutaties.Je kunt hiermee controleren of je permutaties en
combinaties begrepen hebt.
Je krijgt eerst een aantal 'meerkeuzevragen' over telproblemen waarbij de moet kiezen tussen 'combinatie' en 'permutatie'. Daarna volgen een aantal 'open vragen'. Bij de 'open vragen' kan je steeds voor jezelf een antwoord formuleren en dan op 't knopje klikken om te controleren of het klopt. Je gaat dan naar de volgende vraag.
Dat kan ook...:-)
Je krijgt eerst een aantal 'meerkeuzevragen' over telproblemen waarbij de moet kiezen tussen 'combinatie' en 'permutatie'. Daarna volgen een aantal 'open vragen'. Bij de 'open vragen' kan je steeds voor jezelf een antwoord formuleren en dan op 't knopje klikken om te controleren of het klopt. Je gaat dan naar de volgende vraag.
Dat kan ook...:-)
woensdag 9 januari 2013
zaterdag 5 januari 2013
Wat is wiskast?
 Wiskast is de virtuele materialenkast. Je kunt er allerlei wiskundeopdrachten en
activiteiten vinden. Dat kunnen opgaven zijn, DWO-activiteiten, werkstukken,
praktische opdrachten, enz.
Wiskast is de virtuele materialenkast. Je kunt er allerlei wiskundeopdrachten en
activiteiten vinden. Dat kunnen opgaven zijn, DWO-activiteiten, werkstukken,
praktische opdrachten, enz.
Je kunt zelf kiezen welke opdrachten je gaat doen. Via de website kan je je werk inleveren en in de wiskast wordt precies bijgehouden wat je wel en niet gedaan hebt.
Ga naar wiskast voor een overzicht van alle opdrachten en volg de aanwijzingen. Je kunt ook naar mijn wiskast. Dat is een overzicht van de opdrachten die gedaan hebt of opdrachten waar je nog mee bezig bent.
In de les maken we afspraken over het te behalen punten. Sommige opdrachten zijn verplicht. Dit staat in de wiskast duidelijk aangegeven.
Je zou 's kunnen starten met Hoe pak je een wiskundevraagstuk aan? Dat is niet al te ingewikkeld. Je krijgt dan een goed idee hoe 't werkt en hoe een leerroute in een werkruimte gekoppeld kan zijn aan de wiskast.
dinsdag 1 januari 2013
Moet dat niet andersom?
Eén van de leuke vragen op de toets van Taal voor de wiskunde was deze:
Het zou moeten kunnen, maar doe het maar 's...:-)
Zoek twee getallen waarvan de som 10 is en het product 7. Leg uit.Waarop één student voorzichtig kwam vragen of dat niet andersom moest. Opgeteld 7 en vermenigvuldigd 10. Nee, nee... Dat laatste is niet zo moeilijk. Dat kan iedereen. Nee, de som is 10 en het product is 7, dat is andere koek. Wat denk je? Zou het kunnen?
Het zou moeten kunnen, maar doe het maar 's...:-)
Abonneren op:
Posts (Atom)