zaterdag 30 maart 2013
vrijdag 29 maart 2013
maandag 25 maart 2013
zondag 24 maart 2013
Rekenen met kansen
Ik heb een nieuw hoofdstuk toegevoegd aan de samenvattingen:
- voorkennis breuken en combinaties
- de complementregel
- het vaasmodel
- trekken met en zonder terugleggen
- kansen en formules
MathJax
Als \(a \ne 0\) dan heeft de vergelijking \(ax^2 + bx + c = 0\) nul, één of twee oplossingen. Je kunt de oplossingen vinden met de ABC-formule:
\(\eqalign{x = {-b \pm \sqrt{b^2-4ac} \over 2a}}\)
Voorbeeld
\(\frac{1}{2}x^2 - 4x + 1 = 0\)
\(a = \frac{1}{2},\,\,b = - 4\,\,en\,\,c = 1\)
\(x = \frac{{ - - 4 \pm \sqrt {\left( { - 4} \right)^2 - 4 \cdot \frac{1}{2} \cdot 1} }}{{2 \cdot \frac{1}{2}}} = \frac{{4 \pm \sqrt {14} }}{1} = 4 \pm \sqrt {14}\)
\(x = 4 - \sqrt {14} \vee x = 4 + \sqrt {14}\)
Opgelost!
Het bovenstaande is een voorbeeld van MathJax.
\(\eqalign{x = {-b \pm \sqrt{b^2-4ac} \over 2a}}\)
Voorbeeld
\(\frac{1}{2}x^2 - 4x + 1 = 0\)
\(a = \frac{1}{2},\,\,b = - 4\,\,en\,\,c = 1\)
\(x = \frac{{ - - 4 \pm \sqrt {\left( { - 4} \right)^2 - 4 \cdot \frac{1}{2} \cdot 1} }}{{2 \cdot \frac{1}{2}}} = \frac{{4 \pm \sqrt {14} }}{1} = 4 \pm \sqrt {14}\)
\(x = 4 - \sqrt {14} \vee x = 4 + \sqrt {14}\)
Opgelost!
Het bovenstaande is een voorbeeld van MathJax.
maandag 18 maart 2013
donderdag 14 maart 2013
dinsdag 12 maart 2013
maandag 11 maart 2013
Twee driehoeken
Hieronder staan twee driehoeken. Je zou je kunnen afvragen welke van de twee
driehoeken de grootste oppervlakte heeft.
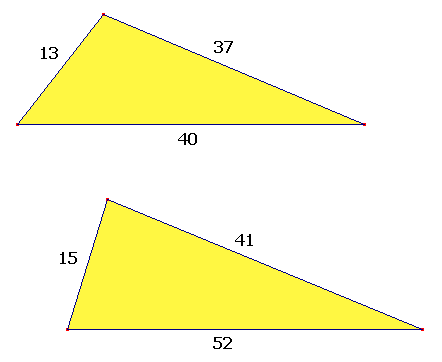
Waarschijnlijk lukt het je niet om de oppervlakte van de driehoeken berekenen... of wel?

Waarschijnlijk lukt het je niet om de oppervlakte van de driehoeken berekenen... of wel?
maandag 4 maart 2013
Abonneren op:
Posts (Atom)