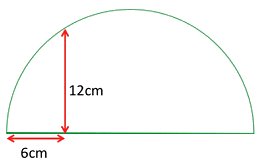
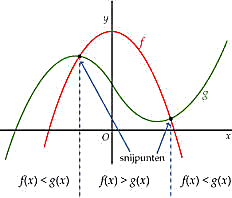
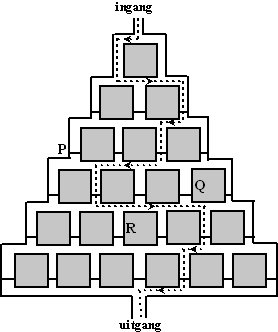
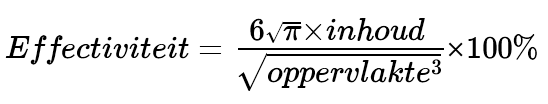Brahmagupta gaf regels voor het sommeren van getallenrijen. Voor de som van de derde machten van de eerste n natuurlijke getallen geeft hij de formule:
\(
\eqalign{1^3 + 2^3 + 3^3 + ... + n^3 = \left( {\frac{{n\left( {n + 1} \right)}}
{2}} \right)^2}
\)
Bewijzen werden er niet gegeven, dus het is onbekend hoe Brahmagupta deze formules heeft gevonden.
bron
Bewijs
\(
\eqalign{
& 1^3 + 2^3 + 3^3 + ... + n^3 = \left( {\frac{{n\left( {n + 1} \right)}}
{2}} \right)^2 \cr
& Neem\,\,n = 1 \cr
& 1^3 = \left( {\frac{{1\left( {1 + 1} \right)}}
{2}} \right)^2 = 1 \cr
& Klopt! \cr
& Neem\,\,n + 1 \cr
& 1^3 + 2^3 + 3^3 + ... + n^3 + \left( {n + 1} \right)^3 = \left( {\frac{{\left( {n + 1} \right)\left( {n + 2} \right)}}
{2}} \right)^2 \cr
& \left( {\frac{{n\left( {n + 1} \right)}}
{2}} \right)^2 + \left( {n + 1} \right)^3 = \left( {\frac{{\left( {n + 1} \right)\left( {n + 2} \right)}}
{2}} \right)^2 \cr
& \frac{1}
{4}n^4 + 1\frac{1}
{2}n^3 + 3\frac{1}
{4}n^2 + 3n + 1 = \frac{1}
{4}n^4 + 1\frac{1}
{2}n^3 + 3\frac{1}
{4}n^2 + 3n + 1 \cr
& Klopt! \cr}
\)