donderdag 29 december 2016
woensdag 28 december 2016
Gebroken exponenten en de rekenregels
Wat dacht je van?
\( \eqalign{\frac{2} {{\root 4 \of 8 }} = \frac{{\root 4 \of {16} }} {{\root 4 \of 8 }} = \root 4 \of 2} \)
Dat kan ook, maar dan heb je geen gebroken exponenten noch rekenregels nodig. Is dat handig of niet?
\( \eqalign{\frac{2} {{\root 4 \of 8 }} = \frac{{\root 4 \of {16} }} {{\root 4 \of 8 }} = \root 4 \of 2} \)
Dat kan ook, maar dan heb je geen gebroken exponenten noch rekenregels nodig. Is dat handig of niet?
zaterdag 24 december 2016
Prettige kerstdagen
\( \eqalign{ & \frac{1} {t} = \frac{1} {a} \Rightarrow t = a \cr & \frac{1} {t} = \frac{1} {a} + \frac{1} {b} \Rightarrow t = \frac{{ab}} {{a + b}} \cr & \frac{1} {t} = \frac{1} {a} + \frac{1} {b} + \frac{1} {c} \Rightarrow t = \frac{{abc}} {{ab + ac + bc}} \cr & \frac{1} {t} = \frac{1} {a} + \frac{1} {b} + \frac{1} {c} + \frac{1} {d} \Rightarrow t = \frac{{abcd}} {{abc + abd + acd + bcd}} \cr} \)
Enzovoort...
zaterdag 17 december 2016
woensdag 14 december 2016
Ik vertrouw op de Heer
Er zit een man tijdens een grote overstroming voor zijn huis. Er komt een vrouw in haar bootje langs en vraagt hem of hij hulp nodig heeft. “Nee, dank u”, zegt de man, “ik vertrouw op de Heer.”
Het water blijft maar stijgen. De man moet zelfs het dak op. Er komt weer een bootje langs, dit keer vol met mensen. Er wordt geroepen: “Stap in, er is nog plaats genoeg.” “Nee, bedankt”, zegt de man, “ik vertrouw op de Heer.”
Er komt een helikopter boven hem hangen en er wordt een touwladder uitgeworpen. “Nee, bedankt. Niet nodig”, roept de man, “ik vertrouw op de Heer”.
Het water stijgt zo hoog dat de man verdrinkt.
In de hemel gekomen vraagt de man aan God: “Waarom heeft U mij niet gered?”
Waarop God antwoordt: “Wat bedoel je? Ik heb twee keer een boot gestuurd en daarna nog een helikopter!”
Het water blijft maar stijgen. De man moet zelfs het dak op. Er komt weer een bootje langs, dit keer vol met mensen. Er wordt geroepen: “Stap in, er is nog plaats genoeg.” “Nee, bedankt”, zegt de man, “ik vertrouw op de Heer.”
Er komt een helikopter boven hem hangen en er wordt een touwladder uitgeworpen. “Nee, bedankt. Niet nodig”, roept de man, “ik vertrouw op de Heer”.
Het water stijgt zo hoog dat de man verdrinkt.
In de hemel gekomen vraagt de man aan God: “Waarom heeft U mij niet gered?”
Waarop God antwoordt: “Wat bedoel je? Ik heb twee keer een boot gestuurd en daarna nog een helikopter!”
Het kleinste gemene veelvoud...
Komt in de onderbouw GGD em KGV voor in de boeken? Maar zag ik dat wel een keer in de voortgangstoets van het CITO? Nou, hoe dan ook... In WisFaq kwam ik deze vraag tegen:
\(
\eqalign{kgv(a,b) = \frac{{ab}}
{{ggd(a,b)}}}
\)
Maar waar laat je het? Welaan, ik zet het maar hier neer.
Meer informatie:
- Wat is het kleinste gemene veelvoud (KGV) van 20 en 28?
- Schrijf de veelvouden van 20 op: 20, 40, 60, 80 ............
- Schrijf de veelvouden van 28 op: 28, 56, 84, 112, ...........
- Kijk welk getal je als eerste in beide rijen ziet staan.
\(
\eqalign{kgv(a,b) = \frac{{ab}}
{{ggd(a,b)}}}
\)
Maar waar laat je het? Welaan, ik zet het maar hier neer.
Meer informatie:
dinsdag 13 december 2016
Hoogleraren
13 december 2016 - In 2015 steeg het aantal vrouwelijke hoogleraren met 0,9%. Het percentage universitair hoofddocenten steeg met 0,7 en het van universitair docenten met 1,6%. Met deze groei duurt het tot 2054 voor er een gelijke m/v-verdeling is onder hoogleraren, blijkt uit de Monitor Vrouwelijke Hoogleraren 2016.
- Eh... sommetje?
zaterdag 10 december 2016
donderdag 8 december 2016
Wiskundeonderwijs
"Mathematics education is much more complicated than you expected even
though you expected it to be more complicated than you expected"
...
woensdag 7 december 2016
Ruimtelijk inzicht
"Als je studenten die een exact vak doen vergelijkt met andere studenten, is er één groot verschil: ze scoren een stuk beter op ruimtelijke vaardigheden. Dus als we als maatschappij meer bèta’s nodig hebben, moeten we stimuleren dat kinderen dat ruimtelijk inzicht ontwikkelen."
bron
bron
maandag 5 december 2016
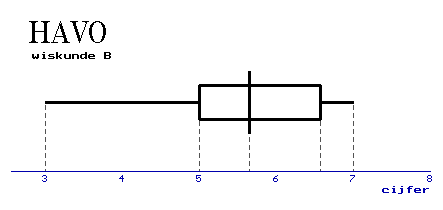
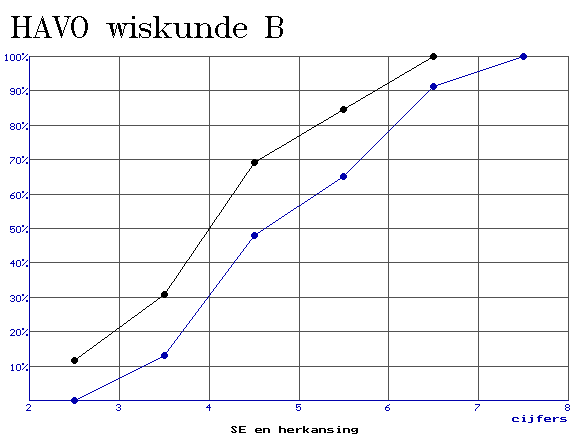
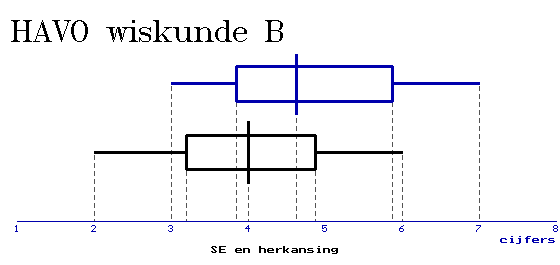
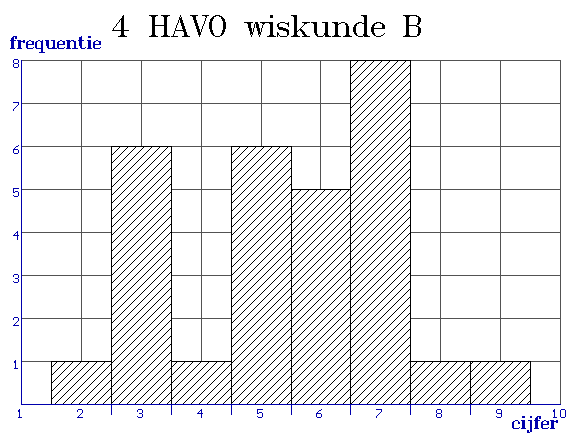
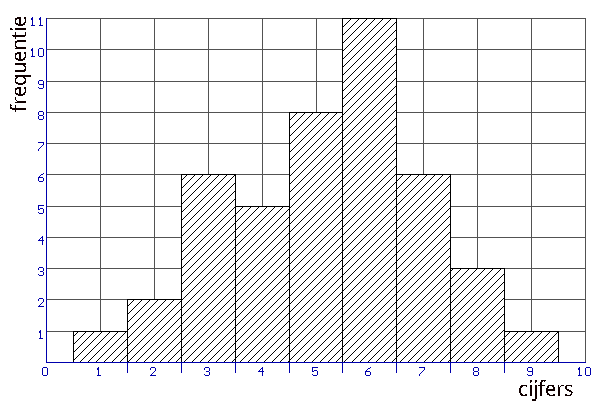
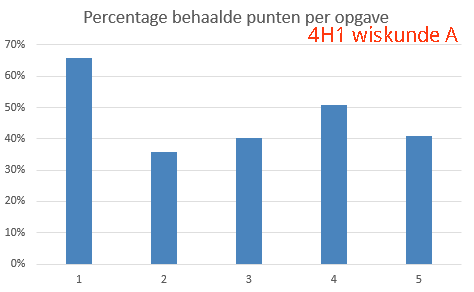
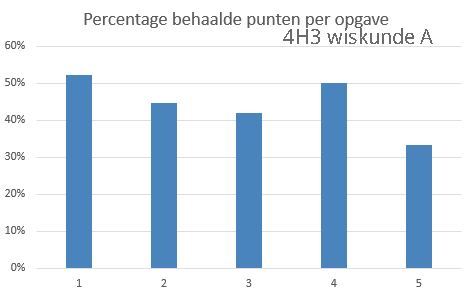
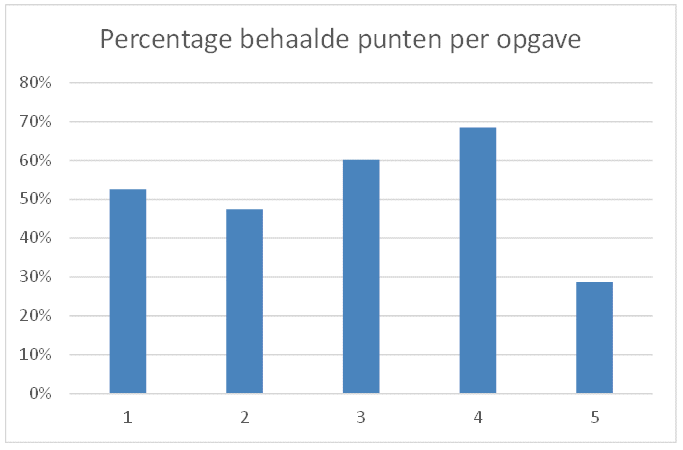
Heeft herkansen zin?
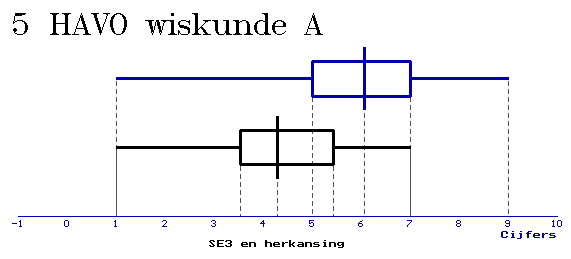
Volgens de formulekaart: "als de boxen elkaar wel overlappen en een mediaan van een boxplot buiten de box van de andere boxplot ligt, dan zeggen we 'het verschil is middelmatig'..." Maar ik word er wel een beetje blij van, ergens...:-)
zondag 4 december 2016
zaterdag 3 december 2016
Week 49

At a party of n people, some pair of people are friends with the same number of people at the party.
donderdag 1 december 2016
Week 48

Laurien, Lennert en Lisanne gingen vogels observeren. Elk van hen zag één vogel die geen van de anderen zag. Elk van hen zag één vogel niet, die beide anderen wel zagen. En één vogel zagen ze alledrie. Van de vogels die Laurien zag, waren er twee geel. Van de vogels die Lennert zag, waren er drie geel. Van de vogels die Lisanne zag, waren er vier geel.
- Hoeveel gele vogels werden er geobserveerd?
(A) 5 (B) 6 (C) 7 (D) 8 (E) 9
woensdag 30 november 2016
dinsdag 29 november 2016
Goniometrische vergelijkingen
In hoofdstuk 8 van Getal & Ruimte van HAVO wiskunde B leren leerlingen o.a. om goniometrische vergelijkingen op te lossen. Zie goniometrische vergelijkingen voor een overzicht. Dat valt nog niet eens mee. Maar deze week heb ik toch weer 's iets ontdekt dat mogelijkerwijs kan helpen.
In het SE stond deze opgave:
Opgave 6
Het idee!?
Voor het berekenen van de hoek zet je je GR in. Dat ziet er dan (bijvoorbeeld) zo uit:
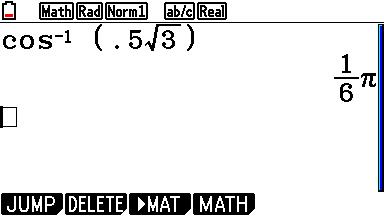
Je hebt dan al de helft van het antwoord te pakken! Met de eenheidscirkel en de cosinuslijn kan je dan de 'andere hoek' bepalen. Je bent dan al een stuk op weg. Mijn idee is dat dit beter werkt dan alles uit je hoofd doen.
In het SE stond deze opgave:
Opgave 6
Geef de exacte waarden van x met \(0 \leqslant x \leqslant 2\pi \)
- \(\cos (x) = \frac{1}{2}\sqrt 3\)
- \(\sin^2 (x + \frac{1}{3}\pi ) = 1\)
- \(\sin (\pi x) = \frac{1}{2}\sqrt 3\)
Het idee!?
Voor het berekenen van de hoek zet je je GR in. Dat ziet er dan (bijvoorbeeld) zo uit:

Je hebt dan al de helft van het antwoord te pakken! Met de eenheidscirkel en de cosinuslijn kan je dan de 'andere hoek' bepalen. Je bent dan al een stuk op weg. Mijn idee is dat dit beter werkt dan alles uit je hoofd doen.
maandag 28 november 2016
zondag 27 november 2016
zondag 13 november 2016
vrijdag 11 november 2016
Week 45
donderdag 10 november 2016
vrijdag 4 november 2016
Dat kan ook...
Toon aan: \(\frac{1}{3} \cdot {}^2\log \left( {4x - 2} \right) = {}^8\log \left( {4x - 2} \right)\)
Een mini-opdracht
Wat zijn merkwaardige producten?
Volgens Wikipedia:
Veel gebruikte merkwaardige producten zijn:
\( \begin{array}{l} \left( {a + b} \right)^2 = a^2 + 2ab + b^2 \\ \left( {a - b} \right)^2 = a^2 - 2ab + b^2 \\ (a + b)(a - b) = a^2 - b^2 \\ \end{array} \)
Op de Wikipedia-pagina staan nog meer merkwaardige producten. Maar deze drie zijn al mooi genoeg...
Volgens Wikipedia:
De benaming merkwaardig product wordt in de algebra gebruikt om enkele
producten aan te duiden die het (be)merken waard zijn, dus waarvan het
goed is ze te onthouden.
Veel gebruikte merkwaardige producten zijn:
\( \begin{array}{l} \left( {a + b} \right)^2 = a^2 + 2ab + b^2 \\ \left( {a - b} \right)^2 = a^2 - 2ab + b^2 \\ (a + b)(a - b) = a^2 - b^2 \\ \end{array} \)
Op de Wikipedia-pagina staan nog meer merkwaardige producten. Maar deze drie zijn al mooi genoeg...
Jippie:-)
\(\begin{array}{l}
{\left( {1\frac{1}{2}} \right)^2} = {\left( {1 + \frac{1}{2}} \right)^2} = {1^2} + 2 \cdot 1 \cdot \frac{1}{2} + {\left( {\frac{1}{2}} \right)^2} = 1 + 1 + \frac{1}{4} = 2\frac{1}{4}\\
{\left( {2\frac{1}{2}} \right)^2} = {\left( {2 + \frac{1}{2}} \right)^2} = {2^2} + 2 \cdot 2 \cdot \frac{1}{2} + {\left( {\frac{1}{2}} \right)^2} = 4 + 2 + \frac{1}{4} = 6\frac{1}{4}\\
{\left( {3\frac{1}{2}} \right)^2} = {\left( {3 + \frac{1}{2}} \right)^2} = {3^2} + 2 \cdot 3 \cdot \frac{1}{2} + {\left( {\frac{1}{2}} \right)^2} = 9 + 3 + \frac{1}{4} = 12\frac{1}{4}\\
...\\
{\left( {n + \frac{1}{2}} \right)^2} = {n^2} + 2 \cdot n \cdot \frac{1}{2} + {\left( {\frac{1}{2}} \right)^2} = {n^2} + n + \frac{1}{4}
\end{array}\)
donderdag 27 oktober 2016
Voor de troepen vooruit lopen

Als je met mensen praat over onderwijs, leren en leerprocessen dan heeft iedereen daar (uiteraard) zo zijn eigen ideeën over. Mijn probleem is meestal dat ik dan steeds maar zit te denken dat wat iedereen ook roept dat mogelijk inderdaad een rol zou kunnen spelen maar het daar steeds maar niet om gaat. De vraag is dan natuurlijk waar gaat het nu eigenlijk om? Wat weten we er nu eigenlijk van? Wat is de essentie?
- Maar ja... doe dat maar 's...:-)
- Dus... ik bedoel maar...:-)
- Dus... ik zeg maar niks...:-)
zaterdag 22 oktober 2016
woensdag 19 oktober 2016
Week 42
Lara zegt tegen haar nichtje: ik ben tweemaal zo oud als jij was, toen ik zo oud was als jij nu bent. En als jij zo oud zal zijn als ik nu, dan zijn we samen 63 jaar.
- Hoe oud zijn beide meisjes nu?
dinsdag 11 oktober 2016
maandag 3 oktober 2016
zondag 2 oktober 2016
zaterdag 1 oktober 2016
Cantor's diagonal elephant
Q: What's big, grey, and proves the uncountability of the reals?
A: Cantor's diagonal elephant
A: Cantor's diagonal elephant
dinsdag 27 september 2016
Jippie!
\(\eqalign{
& \,\,\,\,\,\,\,P\,\,\,\,\,\,\,\,Q\,\,\,\,\,\,\,\,\,\,P \Rightarrow Q \cr
& \overline {\,\,\,\,\,\,\,W\,\,\,\,\,\,W\,\,\,\,\,\,\,\,\,\,\,\,\,\,W\,\,\,\,\,\,\,\,\,} \,\, \cr
& \,\,\,\,\,\,\,W\,\,\,\,\,\,O\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,O\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \cr
& \,\,\,\,\,\,\,O\,\,\,\,\,\,\,W\,\,\,\,\,\,\,\,\,\,\,\,\,\,W \cr
& \underline {\,\,\,\,\,\,\,O\,\,\,\,\,\,\,O\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,W\,\,\,\,\,\,\,\,\,} \cr
& \neg \left( {P \Rightarrow Q} \right) \Leftrightarrow P \wedge \neg Q \cr} \)
maandag 26 september 2016
zaterdag 24 september 2016
dinsdag 20 september 2016
zondag 18 september 2016
Klas 4 wiskunde D
Wat is dat nu?:-)
\( \int \left( - {20 \over \left(4 x\right) ^2 } + {5 \over 4 x}\right)dx = {5 \over 4} \log \left( \left|x\right|\right) + {5 \over 4 x} + C \)
zondag 11 september 2016
Wiskunde 3 HAVO en 3 VWO
Ik heb inmiddels de checklists en de samenvattingen voor klas 3 ook maar weer op wiskundeleraar.nl staan. Zolang er mensen zijn die er iets aan hebben lijkt me dat wel gerechtvaardigd. Alhoewel... eigenlijk niet natuurlijk. Ik ben Gekke Henkie niet... alhoewel... eigenlijk dus wel.
Of ga meteen naar:
Of ga meteen naar:
woensdag 7 september 2016
zaterdag 3 september 2016
woensdag 24 augustus 2016
Week 34
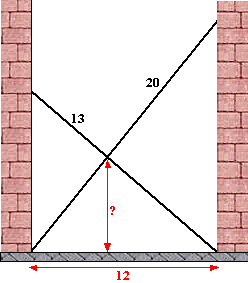
- Op welke hoogte raken de ladders elkaar?
Er zijn nog veel meer vergelijkbare en vragen die net weer heel anders gaan over ladders in een steeg.
donderdag 18 augustus 2016
Het tankstation
Er zijn verschillende varianten van optimaliseringsproblemen die met differentiëren kunnen worden opgelost. De kunst is dan om een formule te bedenken waarmee je (afhankelijk van een variabele) de totale kosten kan berekenen. Zoek het minimum.
Dit is daar een mooi voorbeeld van:
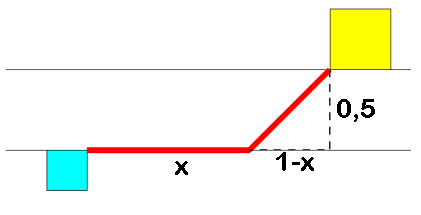
Het idee is dat er tussen 0 en 1 een waarde voor x te vinden is waarbij de kosten voor de aanleg van pijpleiding minimaal zijn.
De formule:
\({K_{totaal}} = 300.000x + 500.000\sqrt {{{\left( {1 - x} \right)}^2} + {{0,5}^2}}\)
Vervolgens kan je de afgeleide bepalen, de afgeleide op nul stellen, oplossen en voila... probleem opgelost. Er komt zelfs een mooi (exact) antwoord uit. Maar hoe doe je dat dan?
De afgeleide:
\(\eqalign{
& {K_{totaal}} = 300.000x + 500.000\sqrt {{{\left( {1 - x} \right)}^2} + {{0,5}^2}} \cr
& {K^|}_{totaal} = 300.000 + 500.000 \cdot \frac{1}{{2\sqrt {{{\left( {1 - x} \right)}^2} + {{0,5}^2}} }} \cdot 2\left( {1 - x} \right) \cdot - 1 \cr
& {K^|}_{totaal} = 300.000 - 500.000 \cdot \frac{{1 - x}}{{\sqrt {{{\left( {1 - x} \right)}^2} + {{0,5}^2}} }} \cr} \)
Stel de afgeleide nul en los de vergelijking op:
\(\eqalign{
& 300.000 - 500.000 \cdot \frac{{1 - x}}{{\sqrt {{{\left( {1 - x} \right)}^2} + {{0,5}^2}} }} = 0 \cr
& 3 - 5 \cdot \frac{{1 - x}}{{\sqrt {{{\left( {1 - x} \right)}^2} + {{0,5}^2}} }} = \cr
& 5 \cdot \frac{{1 - x}}{{\sqrt {{{\left( {1 - x} \right)}^2} + 0,25} }} = 3 \cr
& \frac{{1 - x}}{{\sqrt {{{\left( {1 - x} \right)}^2} + 0,25} }} = \frac{3}{5} \cr
& 5 - 5x = 3\sqrt {{{\left( {1 - x} \right)}^2} + 0,25} \cr
& {(5 - 5x)^2} = 9\left( {{{\left( {1 - x} \right)}^2} + 0,25} \right) \cr
& 25 - 50x + 25{x^2} = 9 - 18x + 9{x^2} + \frac{9}{4} \cr
& 100 - 200x + 100{x^2} = 36 - 72x + 36{x^2} + 9 \cr
& 64{x^2} - 128x + 55 = 0 \cr
& (8x - 5)(8x - 11) = 0 \cr
& x = \frac{5}{8} \vee x = \frac{{11}}{8}\,\,(v.n.) \cr
& x = \frac{5}{8} \cr}\)
Dit is daar een mooi voorbeeld van:

- Een tankstation ligt aan één kant van een rivier van 0,5 km breed. Aan de andere kant van de rivier en 1 km verder stroomafwaarts bevindt zich een bedrijf. Het leggen van pijpleidingen over land kost 300.000 euro/km en onder water 500.000 euro/km. Zoek de voordeligste manier om het bedrijf en het tankstation met pijpleidingen te verbinden.
Het idee is dat er tussen 0 en 1 een waarde voor x te vinden is waarbij de kosten voor de aanleg van pijpleiding minimaal zijn.
De formule:
\({K_{totaal}} = 300.000x + 500.000\sqrt {{{\left( {1 - x} \right)}^2} + {{0,5}^2}}\)
Vervolgens kan je de afgeleide bepalen, de afgeleide op nul stellen, oplossen en voila... probleem opgelost. Er komt zelfs een mooi (exact) antwoord uit. Maar hoe doe je dat dan?
De afgeleide:
\(\eqalign{
& {K_{totaal}} = 300.000x + 500.000\sqrt {{{\left( {1 - x} \right)}^2} + {{0,5}^2}} \cr
& {K^|}_{totaal} = 300.000 + 500.000 \cdot \frac{1}{{2\sqrt {{{\left( {1 - x} \right)}^2} + {{0,5}^2}} }} \cdot 2\left( {1 - x} \right) \cdot - 1 \cr
& {K^|}_{totaal} = 300.000 - 500.000 \cdot \frac{{1 - x}}{{\sqrt {{{\left( {1 - x} \right)}^2} + {{0,5}^2}} }} \cr} \)
Stel de afgeleide nul en los de vergelijking op:
\(\eqalign{
& 300.000 - 500.000 \cdot \frac{{1 - x}}{{\sqrt {{{\left( {1 - x} \right)}^2} + {{0,5}^2}} }} = 0 \cr
& 3 - 5 \cdot \frac{{1 - x}}{{\sqrt {{{\left( {1 - x} \right)}^2} + {{0,5}^2}} }} = \cr
& 5 \cdot \frac{{1 - x}}{{\sqrt {{{\left( {1 - x} \right)}^2} + 0,25} }} = 3 \cr
& \frac{{1 - x}}{{\sqrt {{{\left( {1 - x} \right)}^2} + 0,25} }} = \frac{3}{5} \cr
& 5 - 5x = 3\sqrt {{{\left( {1 - x} \right)}^2} + 0,25} \cr
& {(5 - 5x)^2} = 9\left( {{{\left( {1 - x} \right)}^2} + 0,25} \right) \cr
& 25 - 50x + 25{x^2} = 9 - 18x + 9{x^2} + \frac{9}{4} \cr
& 100 - 200x + 100{x^2} = 36 - 72x + 36{x^2} + 9 \cr
& 64{x^2} - 128x + 55 = 0 \cr
& (8x - 5)(8x - 11) = 0 \cr
& x = \frac{5}{8} \vee x = \frac{{11}}{8}\,\,(v.n.) \cr
& x = \frac{5}{8} \cr}\)
dinsdag 16 augustus 2016
Product-som-methode
Daar was ie weer...:-)
\(\eqalign{
& 4{x^2} - 4x - 3 = 0 \cr
& a \cdot b = - 12 \cr
& a + b = - 4 \cr
& a = - 6\,\,en\,\,b = 2 \cr
& 4{x^2} - 6x + 2x - 3 = 0 \cr
& 2x(2x - 3) + 2x - 3 = 0 \cr
& (2x + 1)(2x - 3) = 0 \cr
& 2x + 1 = 0 \vee 2x - 3 = 0 \cr
& 2x = - 1 \vee 2x = 3 \cr
& x = - \frac{1}{2} \vee x = 1\frac{1}{2} \cr}\)
...ik ken nog meer kunstjes, maar dit is wel mijn favoriet...:-)
\(\eqalign{
& 4{x^2} - 4x - 3 = 0 \cr
& a \cdot b = - 12 \cr
& a + b = - 4 \cr
& a = - 6\,\,en\,\,b = 2 \cr
& 4{x^2} - 6x + 2x - 3 = 0 \cr
& 2x(2x - 3) + 2x - 3 = 0 \cr
& (2x + 1)(2x - 3) = 0 \cr
& 2x + 1 = 0 \vee 2x - 3 = 0 \cr
& 2x = - 1 \vee 2x = 3 \cr
& x = - \frac{1}{2} \vee x = 1\frac{1}{2} \cr}\)
...ik ken nog meer kunstjes, maar dit is wel mijn favoriet...:-)
zaterdag 16 juli 2016
Dat is ook toevallig... of misschien ook wel niet...
Ik las ergens dat \(\sqrt {2\frac{2}{3}}\) hetzelfde is als \(2\sqrt {\frac{2}{3}}\). De vraag is dan "is dat altijd zo?" en "zo nee, kan je nog meer voorbeelden bedenken?" of nog beter "kun je alle mogelijkheden geven?".
Je moet dan nog wel even bepalen wat nu precies de bijzonderheid is van het voorbeeld. Kortom (zoals altijd) is er (mogelijkerwijs) van alles te ontdekken.
Maar helaas... 't is vakantie... dus dan houdt alles op:-)
Naschrift
Nou vooruit... hier is er nog één....\(\sqrt {3\frac{3}{8}} = 3\sqrt {\frac{3}{8}}\)
Nog meer naschrift
\(\eqalign{
& \sqrt {2\frac{2}{3}} \to \frac{2}{3}\sqrt 6 \cr
& 2\sqrt {\frac{2}{3}} \to \frac{2}{3}\sqrt 6 \cr
& \sqrt {3\frac{3}{8}} \to \frac{3}{4}\sqrt 6 \cr
& 3\sqrt {\frac{3}{8}} \to \frac{3}{4}\sqrt 6 \cr}\)
Maar nu stop ik er mee hoor...:-)
Maak het verhaal zelf af en kleur de plaatjes...
Je moet dan nog wel even bepalen wat nu precies de bijzonderheid is van het voorbeeld. Kortom (zoals altijd) is er (mogelijkerwijs) van alles te ontdekken.
Maar helaas... 't is vakantie... dus dan houdt alles op:-)
Naschrift
Nou vooruit... hier is er nog één....\(\sqrt {3\frac{3}{8}} = 3\sqrt {\frac{3}{8}}\)
Nog meer naschrift
\(\eqalign{
& \sqrt {2\frac{2}{3}} \to \frac{2}{3}\sqrt 6 \cr
& 2\sqrt {\frac{2}{3}} \to \frac{2}{3}\sqrt 6 \cr
& \sqrt {3\frac{3}{8}} \to \frac{3}{4}\sqrt 6 \cr
& 3\sqrt {\frac{3}{8}} \to \frac{3}{4}\sqrt 6 \cr}\)
Maar nu stop ik er mee hoor...:-)
Maak het verhaal zelf af en kleur de plaatjes...
woensdag 13 juli 2016
Week 28
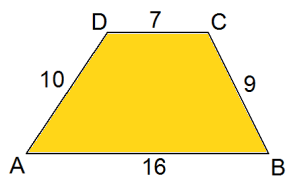
Gegeven is het trapezium ABCD met:
- AB=16, BC=9, DC=7 en AD=10.
-
AB //
DC
zaterdag 9 juli 2016
Eindejaarsevaluatie algemeen:-)
Hierbij verklaar ik het schooljaar 2015-2016 voor beëindigd. Het was, zoals altijd, een bewogen jaar.:-)
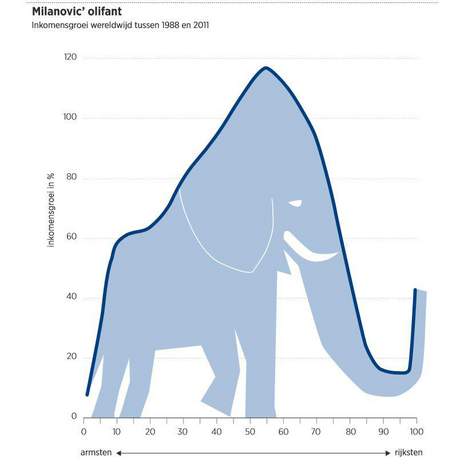
Ik heb les gegeven, iets gedaan met doodlopende leerlijnen, een lach, een traan, getwijfeld of ik het op zou geven, maar toch maar doorgegaan. Het plan is om me verder te ontwikkelen, het moet nu maar een keer van komen. Zoek de olifant!

...en dan... ga ik dat maar doen volgend jaar. Les geven, studeren, aansturen, overleggen, DWO opnieuw starten... PO voor wiskunde A verbeteren... maar nu eerst vakantie vieren.
Ik heb les gegeven, iets gedaan met doodlopende leerlijnen, een lach, een traan, getwijfeld of ik het op zou geven, maar toch maar doorgegaan. Het plan is om me verder te ontwikkelen, het moet nu maar een keer van komen. Zoek de olifant!

...en dan... ga ik dat maar doen volgend jaar. Les geven, studeren, aansturen, overleggen, DWO opnieuw starten... PO voor wiskunde A verbeteren... maar nu eerst vakantie vieren.
woensdag 6 juli 2016
't Blijft leuk:-)
\(\eqalign{
& 4{x^2} - 24x - 85 \cr
& 4\cdot - 85 = - 340 \cr
& - 34 \cdot 10 = - 340 \cr
& - 34 + 10 = - 24 \cr
& 4{x^2} - 34x + 10x - 85 = \cr
& 2x(2x - 17) + 5(2x - 17) = \cr
& (2x + 5)(2x - 17) \cr} \)
maandag 4 juli 2016
maandag 27 juni 2016
Zes maken
\(
\eqalign{
& (0! + 0! + 0!)! = 6 \cr
& (1 + 1 + 1)! = 6 \cr
& 2 + 2 + 2 = 6 \cr
& \sqrt 3 \cdot \left( {\sqrt 3 + \sqrt 3 } \right) = 6 \cr
& \sqrt 4 + \sqrt 4 + \sqrt 4 = 6 \cr
& 5^0 + \sqrt 5 \cdot \sqrt 5 = 6 \cr
& 6 - 6 + 6 = 6 \cr
& 7 - (7:7) = 6 \cr
& \root 3 \of 8 + \root 3 \of 8 + \root 3 \of 8 = 6 \cr
& (9 + 9):\sqrt 9 = 6 \cr}
\)
woensdag 15 juni 2016
Verdiepingsopdracht
Dit zou een aardige opdracht zijn (geweest) voor wiskunde D.
 Van n3 witte kubusjes bouw je een grote kubus van n bij n bij n.
Van n3 witte kubusjes bouw je een grote kubus van n bij n bij n.
De buitenkant van deze grote kubus kleur je rood. De kubus wordt weer afgebroken...
Er zijn nu verschillende kubusjes: witte kubusjes, kubusjes met 1 rood vlak, kubusjes met 2 rode vlakken en er zijn zelfs kubusjes met 3 rode vlakken.
Je kiest nu willekeurig een kubusje en met dat kubusje wordt gedobbeld.
 Van n3 witte kubusjes bouw je een grote kubus van n bij n bij n.
Van n3 witte kubusjes bouw je een grote kubus van n bij n bij n.De buitenkant van deze grote kubus kleur je rood. De kubus wordt weer afgebroken...
Er zijn nu verschillende kubusjes: witte kubusjes, kubusjes met 1 rood vlak, kubusjes met 2 rode vlakken en er zijn zelfs kubusjes met 3 rode vlakken.
Je kiest nu willekeurig een kubusje en met dat kubusje wordt gedobbeld.
- Bereken de kans dat de een rood zijvlak boven komt te liggen.
- Probleemaanpak, formules, kansrekenen, volhouden... maar helaas...
Een bijzonder vergelijking
Eigenlijk zijn alle vergelijkingen bijzonder, maar soms kom je wel 's dingen tegen die je opvallen. In WisFaq:
Er zit wel een soort herhaling in. Iets met 4 en 9. Dat is dan ook meteen de oplossing omdat je voor 4x3-9x2+4x-9 kunt schrijven x²(4x-9)+4x-9. Dat geeft:
x²(4x-9)+4x-9=0
(4x-9)(x²+1)=0
4x-9=0 of x²+1=0 (v.n.)
x=2\(\frac{1}{4}\)
Opgelost...:-)
- Hoe ik 4x3-9x2+4x-9=0 moet oplossen?
Er zit wel een soort herhaling in. Iets met 4 en 9. Dat is dan ook meteen de oplossing omdat je voor 4x3-9x2+4x-9 kunt schrijven x²(4x-9)+4x-9. Dat geeft:
x²(4x-9)+4x-9=0
(4x-9)(x²+1)=0
4x-9=0 of x²+1=0 (v.n.)
x=2\(\frac{1}{4}\)
Opgelost...:-)
donderdag 9 juni 2016
Totaal overzicht HAVO wiskunde A
Totaal overzicht HAVO wiskunde B
dinsdag 7 juni 2016
Kamer overstag: toch 20 uur les voor docent
"Drie keer sinds eind 2014 diende D66-Kamerlid Paul van Meenen zijn motie in, drie keer werd die weggestemd. Vandaag, bij de vierde poging, gaat het wel lukken. Een Kamermeerderheid zal het streven steunen naar maximaal 20 lesuren voor een fulltime-docent in het voortgezet onderwijs en maximaal acht dagdelen lesgeven voor een voltijds leraar in het basisonderwijs."
"Een Kamermeerderheid zal het streven steunen naar maximaal 20 lesuren...." - eh... o ja joh? Vanaf 2032 zeker..!?:-) #datkannietgoedgaan
...maar hoe dan ook... die 20 lesuren...!? Dat gaat echt niet gebeuren... je zult het zien... #irestmycase #readmylips
"Een Kamermeerderheid zal het streven steunen naar maximaal 20 lesuren...." - eh... o ja joh? Vanaf 2032 zeker..!?:-) #datkannietgoedgaan
...maar hoe dan ook... die 20 lesuren...!? Dat gaat echt niet gebeuren... je zult het zien... #irestmycase #readmylips
vrijdag 3 juni 2016
Probleemaanpak deel 4 (slot)
Vandaag hebben we de laatste les probleemaanpak gedaan. De eindtoets. Er waren nog wel wat 'hints' nodig zo hier en daar, maar verder ging het heel goed. Het was in ieder geval mooi om te zien dat 'sommige dingen' die eerst nog niet zo 'vanzelfsprekend' waren nu al beter gingen.
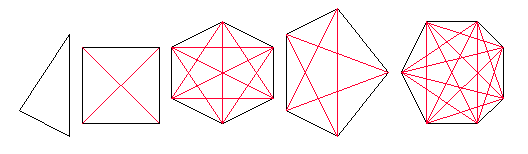
Ik ga de proeven in het weekend nakijken en misschien schrijf ik er nog wel iets meer over. Ik vond het in ieder geval een geslaagd project, 't is leerzaam en er wordt hard gewerkt, nagedacht en problemen opgelost!:-)

Ik ga de proeven in het weekend nakijken en misschien schrijf ik er nog wel iets meer over. Ik vond het in ieder geval een geslaagd project, 't is leerzaam en er wordt hard gewerkt, nagedacht en problemen opgelost!:-)
- Krant
- Maximale oppervlakte driehoek
- Hoeveel diagonalen heeft een n-hoek?
- De wijzers van de klok
- ...
- ...
woensdag 1 juni 2016
Probleemaanpak deel 3
Vandaag hebben de volgende opdrachten gedaan:
twee metselaars
Twee metselaars bouwen samen aan één toren. Ze doen er 20 uur over. Als ze elk apart een toren bouwen doet de ene er 9 uur langer over dan de andere.
twee slakken
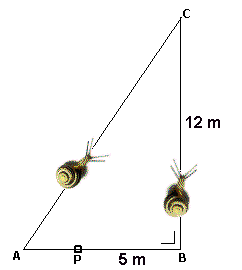
Twee slakken lopen allebei vanaf punt P naar C over de zijden van een rechthoekige driehoek. De ene slak loopt linksom en de andere slak loopt rechtsom. Als de slakken even hard lopen komen ze precies tegelijkertijd in C aan. PB=5m en BC=12m.
kubusjes
 Van n3 witte kubusjes bouw je een grote kubus van n bij n bij n.
Van n3 witte kubusjes bouw je een grote kubus van n bij n bij n.
De buitenkant van deze grote kubus kleur je rood. De kubus wordt weer afgebroken...
Er zijn nu verschillende kubusjes. Witte kubusjes, kubusjes met 1 rood vlak, kubusjes met 2 rode vlakken en er zijn zelfs kubusjes met 3 rode vlakken.
Naschrift
't Was nog aardig om vast te stellen dat voor Lower=-100 en Upper=0 de GR nog een oplossing heeft gevonden voor de twee metselaars. x=-5 is ook een oplossing. Dus de ene metselaar doet er -5 uur over om een toren te bouwen. Dat betekent dat hij 5 uur nodig heeft om een toren af te breken. Als de andere metselaar er 4 uur over doet om een toren te bouwen dan hebben na 20 uur kennelijk toch een toren af.:-)
Tenslotte de oefentoets uitgedeeld met uitwerkingen. Vrijdag a.s. doen we dan de echte toets in tweetallen.
twee metselaars

Twee metselaars bouwen samen aan één toren. Ze doen er 20 uur over. Als ze elk apart een toren bouwen doet de ene er 9 uur langer over dan de andere.
- Hoe lang doet elk over het bouwen van 1 toren?
twee slakken

Twee slakken lopen allebei vanaf punt P naar C over de zijden van een rechthoekige driehoek. De ene slak loopt linksom en de andere slak loopt rechtsom. Als de slakken even hard lopen komen ze precies tegelijkertijd in C aan. PB=5m en BC=12m.
- Bereken exact de lengte van AP.
kubusjes
 Van n3 witte kubusjes bouw je een grote kubus van n bij n bij n.
Van n3 witte kubusjes bouw je een grote kubus van n bij n bij n.De buitenkant van deze grote kubus kleur je rood. De kubus wordt weer afgebroken...
Er zijn nu verschillende kubusjes. Witte kubusjes, kubusjes met 1 rood vlak, kubusjes met 2 rode vlakken en er zijn zelfs kubusjes met 3 rode vlakken.
- Hoeveel kubusjes zijn er van elk soort uitgedrukt in n?
Naschrift
't Was nog aardig om vast te stellen dat voor Lower=-100 en Upper=0 de GR nog een oplossing heeft gevonden voor de twee metselaars. x=-5 is ook een oplossing. Dus de ene metselaar doet er -5 uur over om een toren te bouwen. Dat betekent dat hij 5 uur nodig heeft om een toren af te breken. Als de andere metselaar er 4 uur over doet om een toren te bouwen dan hebben na 20 uur kennelijk toch een toren af.:-)
Tenslotte de oefentoets uitgedeeld met uitwerkingen. Vrijdag a.s. doen we dan de echte toets in tweetallen.
vrijdag 27 mei 2016
Probleemaanpak deel 2
We hebben vandaag probleemaanpak II gedaan. Puzzel, vliegtuig en piano.
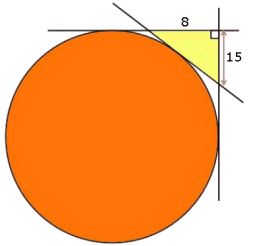
een vierkant en een cirkel
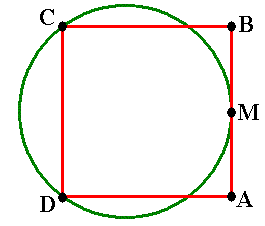
Het rode vierkant heeft een zijde van 8. Het punt M is het midden van AB en de groene cirkel gaat door de punten C, D en M.
't Is even puzzelen misschien maar de vorige keer hadden we al gezien dat bij een cirkel het middelpunt belangrijk is en dat als je hier en daar de straal tekent je voor je 't weet er uit komt.... misschien:-)
het vliegtuig

Een vliegtuig vliegt van Amsterdam naar Moskou met een gemiddelde snelheid van 800 km/uur. Op de terugweg heeft het de wind tegen en haalt het (gemiddeld) niet meer dan 600 km/uur.
't Zal toch wel niet 700 km/u zijn. Dat is te makkelijk. Je kunt een concreet voorbeeld nemen (neem bijvoorbeeld voor de afstand 2400 km), los het op en ga nadenken of het antwoord voor elke afstand geldt.
drie dochters
 Twee mannen lopen op straat. A zegt 'ik weet een leuk raadsel'.
Twee mannen lopen op straat. A zegt 'ik weet een leuk raadsel'.
B zegt 'zeg op'.
A zegt 'ik heb 3 dochters en het product van hun leeftijden is 36. Hoe oud zijn ze?
B zegt 'dan weet ik het nog niet'.
A zegt 'ik geef je nog een hint: het huisnummer aan de overkant is de som van hun leeftijden'.
B zegt 'dan weet ik het nog niet'.
A zegt 'ok, laatste aanwijzing: mijn oudste dochter speelt piano'.
een vierkant en een cirkel

Het rode vierkant heeft een zijde van 8. Het punt M is het midden van AB en de groene cirkel gaat door de punten C, D en M.
- Bereken exact de straal van deze cirkel
't Is even puzzelen misschien maar de vorige keer hadden we al gezien dat bij een cirkel het middelpunt belangrijk is en dat als je hier en daar de straal tekent je voor je 't weet er uit komt.... misschien:-)
het vliegtuig

Een vliegtuig vliegt van Amsterdam naar Moskou met een gemiddelde snelheid van 800 km/uur. Op de terugweg heeft het de wind tegen en haalt het (gemiddeld) niet meer dan 600 km/uur.
- Bereken de gemiddelde snelheid over de gehele tocht.
't Zal toch wel niet 700 km/u zijn. Dat is te makkelijk. Je kunt een concreet voorbeeld nemen (neem bijvoorbeeld voor de afstand 2400 km), los het op en ga nadenken of het antwoord voor elke afstand geldt.
drie dochters
 Twee mannen lopen op straat. A zegt 'ik weet een leuk raadsel'.
Twee mannen lopen op straat. A zegt 'ik weet een leuk raadsel'.B zegt 'zeg op'.
A zegt 'ik heb 3 dochters en het product van hun leeftijden is 36. Hoe oud zijn ze?
B zegt 'dan weet ik het nog niet'.
A zegt 'ik geef je nog een hint: het huisnummer aan de overkant is de som van hun leeftijden'.
B zegt 'dan weet ik het nog niet'.
A zegt 'ok, laatste aanwijzing: mijn oudste dochter speelt piano'.
- Hoe oud zijn die dochters?
Dit is vooral om te laten zien dat het soms handig kan zijn om alle mogelijke oplossing na te gaan. Dat lijkt mischien veel werk, maar hier is dat goed te doen. Misschien ook nog aardig om te bedenken dat je soms iets niet weet maar dat dat dan ook kennis is en dat je dan wat andere dingen wel weer weet...:-)
Nou ja... de tijd vloog om, uitwerkingen uitgedeeld... en dan nog 10 minuten over om met de telefoon te spelen, want dat moet natuurlijk ook gebeuren...
Abonneren op:
Posts (Atom)