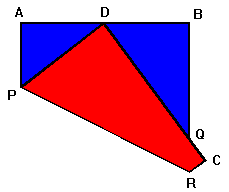
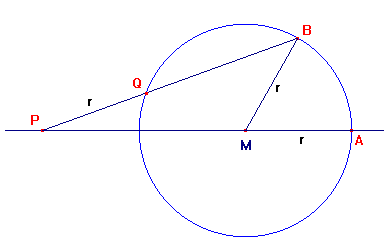
een vierkant en een cirkel
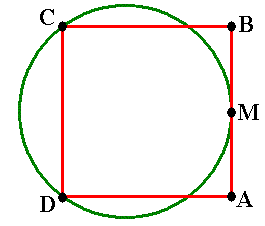
Het rode vierkant heeft een zijde van 8. Het punt M is het midden van AB en de groene cirkel gaat door de punten C, D en M.
- Bereken exact de straal van deze cirkel
't Is even puzzelen misschien maar de vorige keer hadden we al gezien dat bij een cirkel het middelpunt belangrijk is en dat als je hier en daar de straal tekent je voor je 't weet er uit komt.... misschien:-)
het vliegtuig

Een vliegtuig vliegt van Amsterdam naar Moskou met een gemiddelde snelheid van 800 km/uur. Op de terugweg heeft het de wind tegen en haalt het (gemiddeld) niet meer dan 600 km/uur.
- Bereken de gemiddelde snelheid over de gehele tocht.
't Zal toch wel niet 700 km/u zijn. Dat is te makkelijk. Je kunt een concreet voorbeeld nemen (neem bijvoorbeeld voor de afstand 2400 km), los het op en ga nadenken of het antwoord voor elke afstand geldt.
drie dochters
 Twee mannen lopen op straat. A zegt 'ik weet een leuk raadsel'.
Twee mannen lopen op straat. A zegt 'ik weet een leuk raadsel'.B zegt 'zeg op'.
A zegt 'ik heb 3 dochters en het product van hun leeftijden is 36. Hoe oud zijn ze?
B zegt 'dan weet ik het nog niet'.
A zegt 'ik geef je nog een hint: het huisnummer aan de overkant is de som van hun leeftijden'.
B zegt 'dan weet ik het nog niet'.
A zegt 'ok, laatste aanwijzing: mijn oudste dochter speelt piano'.
- Hoe oud zijn die dochters?
Dit is vooral om te laten zien dat het soms handig kan zijn om alle mogelijke oplossing na te gaan. Dat lijkt mischien veel werk, maar hier is dat goed te doen. Misschien ook nog aardig om te bedenken dat je soms iets niet weet maar dat dat dan ook kennis is en dat je dan wat andere dingen wel weer weet...:-)
Nou ja... de tijd vloog om, uitwerkingen uitgedeeld... en dan nog 10 minuten over om met de telefoon te spelen, want dat moet natuurlijk ook gebeuren...